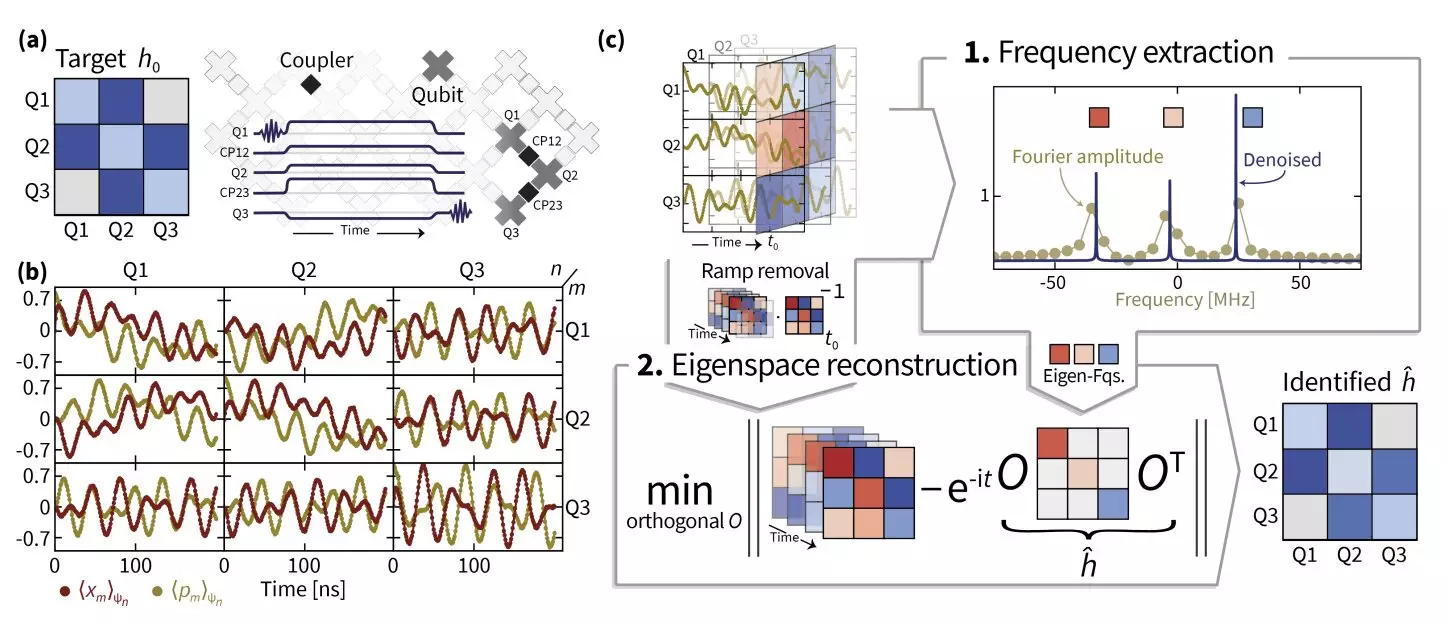
The frontier of quantum computing offers the tantalizing promise of performing complex simulations far beyond the capabilities of classical systems. Researchers from Freie Universität Berlin, the University of Maryland, NIST, Google AI, and Abu Dhabi have took a significant step toward this goal, particularly concerning the accurate estimation of Hamiltonian parameters in bosonic excitations utilizing a superconducting quantum simulator. In a pivotal article available on arXiv, they laid out groundbreaking methodologies that could redefine the scope of quantum simulations, facilitating explorations of intricate quantum phenomena that were previously considered unattainable.
At a conference in Brazil, Jens Eisert, the principal investigator of the study, received an unexpected call from collaborateurs at Google AI. They faced daunting challenges while calibrating their Sycamore superconducting quantum chip, and they needed assistance with Hamiltonian learning methodologies. What initially appeared to be a routine call quickly transformed into a complex puzzle, igniting Eisert’s intrigue in the problem’s underlying nature. Despite his previous experience in the field, he soon discovered that realizing the goals of the project was far more intricate than anticipated, especially when confronting the difficulties in accurately recovering the Hamiltonian frequencies required for system identification.
Eisert’s journey took an innovative turn with the collaboration of two Ph.D. students, Ingo Roth and Dominik Hangleiter. Together, they mulled over different solutions, ultimately employing advanced techniques such as superresolution, which enhances eigenvalue estimation, to decipher the elusive Hamiltonian parameters. The journey was marked by years of iterative experimentation. The eventual inclusion of Jonas Fuksa, another bright mind, and the unwavering support from Pedram Roushan, the experimental lead, shaped the evolution of their work, leading them to eventual success.
In the process of decoding the Hamiltonian dynamics within the superconducting quantum simulator, the researchers employed various pivotal techniques. Superresolution formed the backbone of their approach, allowing for enhanced resolution in eigenvalue estimation, which subsequently resulted in more accurate Hamiltonian frequency detection. The use of manifold optimization represented another quantum leap, enabling the team to recover the eigenspaces of the Hamiltonian operator itself. This is particularly critical, as manifold optimization applies specialized algorithms to address issues within curved spaces rather than conventional Euclidean systems, which often doesn’t suffice in complex quantum scenarios.
Eisert notes, “To attain robust estimates, we combined a number of ideas.” He elaborates on the importance of understanding the processes related to the switching on and off of quantum systems, as these actions are often non-trivial and flawed in real-world applications. This led to chaotic results when trying to model a Hamiltonian evolution that was not purely Hamiltonian. Consequently, the team’s innovation, termed TensorEsprit, emerged as a novel signal processing method that proved particularly effective for recovering Hamiltonian parameters across large system sizes.
Contributions to Quantum Theory and Applications
The culmination of their work manifested in a robust sequence of techniques enabling the identification of Hamiltonian parameters associated with as many as 14 coupled superconducting qubits across dual Sycamore processors. Their initial findings suggested a promising scalability of these methodologies, hinting that they could be applicable to larger quantum processor frameworks. Eisert’s reflections highlight an essential understanding within quantum mechanics: while Hamiltonians define a system’s behavior, they are often assumed known when they may not be, thereby complicating predictive capacities.
The implications of their research extend far beyond theoretical advancements. By contributing substantially to the understanding of Hamiltonian operators, their efforts could catalyze breakthroughs in the development of practical quantum technologies. Specifically, enhancing the characterization of analog quantum simulators may lead to unprecedented precision in quantum simulations, opening potential pathways to explore novel quantum materials and systems never before reachable through classical methods.
Future Directions in Hamiltonian Learning
Looking to the horizon, Eisert and his team are poised to apply their methodologies to more intricate interacting quantum systems. They are exploring the incorporation of tensor network methodologies into scenarios involving cold atoms, a concept first explored by physicist Immanuel Bloch. Eisert’s optimism about the future of Hamiltonian learning underscores the significance of identifying Hamiltonians through empirical data, reinforcing the notion that successful quantum experiments hinge critically on this understanding.
The strides made by Eisert and his colleagues not only advance theoretical quantum physics but have the potential to influence practical applications in quantum computing. By enabling high-fidelity analog simulations, their research underscores the incredible possibilities that lie in waiting as our comprehension of quantum systems continues to mature, ultimately reshaping the practical landscape of quantum technologies.